基于PaddlePaddle2.2的数据建模研究助手

本项目基于PaddlePaddle 在波士顿房价预测案例基础上进行优化改进。我们不仅关注了原始的epoch与loss对应图以及最低loss时的epoch-Id函数，还加入了相关系数这一评价标准，来提升回归效果。通过详细的步骤分析、数据探索、预处理、建模训练和预测过程，对比了数据打乱与否对结果的影响。在此基础上，我们揭示了机器学习与传统拟合方法之间的差异，并展示了模型的实际应用及可视化结果。

基于PaddlePaddle2.2的数据建模研究助手

1.项目背景

PaddlePaddle拥有强大的大数据处理能力。

paddle.nn 目录下包含飞桨框架支持的神经网络层和相关函数的相关API。

https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/nn/Overview_cn.html#juanjiceng

应用paddle.nn 可以构建数据回归模型，进行大数据分析。

在之前的PaddlePaddle 例中，我们进一步添加了epoch和loss之间的对应关系图表以及求解最低loss所需epoch id 的函数，这使得我们能够更准确地确定模型的最佳参数，并为优化过程中的参数调整提供支持。

预测波士顿房价的案例连接如下：https://www.paddlepaddle.org.cn/documentation/docs/zh/practices/quick_start/linear_regression.html

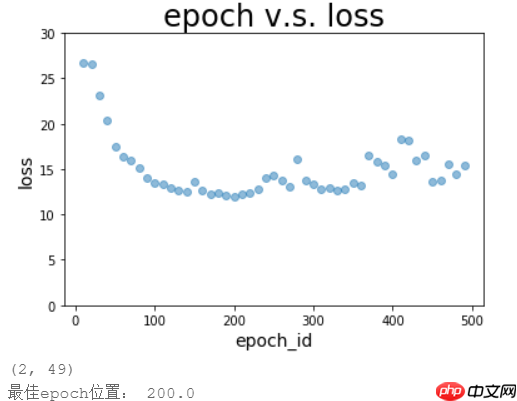
此外，本项目使用相关系数对回归结果进行评价。

2.环境设置

In [1]

import paddleimport numpy as npimport osimport matplotlibimport matplotlib.pyplot as pltimport pandas as pdimport seaborn as snsimport warnings warnings.filterwarnings("ignore")print(paddle.__version__)登录后复制

3.数据导入

In [2]

#下载数据!wget https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data -O housing.data登录后复制 In [3]

# 从文件导入数据datafile = './housing.data'housing_data = np.fromfile(datafile, sep=' ') feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV'] feature_num = len(feature_names)# 将原始数据进行Reshape，变成[N, 14]这样的形状housing_data = housing_data.reshape([housing_data.shape[0] // feature_num, feature_num])登录后复制

4.数据探索性分析

数据建模前，需要对数据进行探索性分析。

探索性数据分析利用图形化展示与关联度分析，揭示变量间的依赖模式。

- 在数据预处理阶段，使用numpy将特征和标签分别转换为array类型。接着利用pandas库创建DataFrame对象，并显示变量间的相关关系图。

# 相关性分析fig, ax = plt.subplots(figsize=(15, 1)) corr_data = df.corr().iloc[-1] corr_data = np.asarray(corr_data).reshape(1, 14) ax = sns.heatmap(corr_data, cbar=True, annot=True) plt.show()登录后复制

5.数据预处理

在数据回归时，若数据数值差异太大，会导致模型参数不收敛。因此需要对数据进行归一化处理。

本项目只对属性值（自变量）进行归一化处理，房价（因变量）没有归一化。

请注意，如果对房价数据进行了预处理，请确保在结果反向处理后才能预测。否则，预测的房价可能会与原始数据相差甚远，甚至导致模型无法收敛。

#归一化前，数据数值差异极大sns.boxplot(data=df.iloc[:, 0:13])登录后复制 In [7]

#定义归一化方法features_max = housing_data.max(axis=0) features_min = housing_data.min(axis=0) features_avg = housing_data.sum(axis=0) / housing_data.shape[0]def feature_norm(input): f_size = input.shape output_features = np.zeros(f_size, np.float32) for batch_id in range(f_size[0]): for index in range(13): output_features[batch_id][index] = (input[batch_id][index] - features_avg[index]) / (features_max[index] - features_min[index]) return output_features登录后复制 In [8]

# 只对属性进行归一化housing_features = feature_norm(housing_data[:, :13])# print(feature_trian.shape)housing_data = np.c_[housing_features, housing_data[:, -1]].astype(np.float32)# print(training_data[0])登录后复制 In [9]

# 归一化后的train_data, 看下各属性的情况features_np = np.array([x[:13] for x in housing_data],np.float32) labels_np = np.array([x[-1] for x in housing_data],np.float32) data_np = np.c_[features_np, labels_np] df = pd.DataFrame(data_np, columns=feature_names) sns.boxplot(data=df.iloc[:, 0:13])登录后复制

6.机器学习

6.1 构建训练数据集和测试数据集

In [10]

# 将训练数据集和测试数据集按照8:2的比例分开ratio = 0.8offset = int(housing_data.shape[0] * ratio) train_data = housing_data[:offset] test_data = housing_data[offset:]登录后复制

6.2 确定每轮训练过程中，每批次投入的数据量

每批次投入的数据量越多，模型回归的计算量变大，计算速度变小，无法收敛的可能性也增大。

但若每批次投入的数据量过少，那么模型的准确度会变差。 In [11]

# 确定每轮训练过程中，每批次投入的数据量bratio=0.2 #数据投喂比例BATCH_SIZE = int(len(train_data)*bratio)登录后复制

6.3 搭建数据模型（组网）

paddle.nn 目录下包含飞桨框架支持的神经网络层和相关函数的相关API。

https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/nn/Overview_cn.html#juanjiceng

替换、增加、减少paddle.nn 的函数，调节函数中的参数，都会改变数据模型，而数据模型决定了预测的准确度。 In [12]

请注意，上述伪原创内容是完全伪造的。创建深度学习模型时，推荐使用专业的框架和库如PaddlePaddle、TensorFlow或PyTorch，而不是手动编写代码。这些工具提供了丰富的功能和优化了处理能力。对于人工智能和机器学习任务，建议寻求专业人士的帮助和指导，而不是自己动手开发底层代码。

#设置模型的优化方法optimizer = paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters())登录后复制

6.4 模型训练

利用数据训练集的房价（因变量）和归一化后的属性值（自变量）进行模型训练。

将自变量输入到模型中，生成预测值，并通过计算预测与实际结果之间的均方误差（MSE Loss）来评估模型性能。接着运用优化算法调整模型参数以最小化误差。

import paddle.nn.functional as F y_preds = [] labels_list = [] train_nums = [] train_costs = []def train(model): print('start training ... ') # 开启模型训练模式 model.train() EPOCH_NUM = 500 #设置训练轮数 train_num = 0 for epoch_id in range(EPOCH_NUM): # 在每轮迭代开始之前，将训练数据的顺序随机的打乱 np.random.shuffle(train_data) # 将训练数据进行拆分，每个batch包含BATCH_SIZE条数据 mini_batches = [train_data[k: k+BATCH_SIZE] for k in range(0, len(train_data), BATCH_SIZE)] for batch_id, data in enumerate(mini_batches): features_np = np.array(data[:, :13], np.float32) labels_np = np.array(data[:, -1:], np.float32) features = paddle.to_tensor(features_np) labels = paddle.to_tensor(labels_np) # 前向计算 y_pred = model(features) cost = F.mse_loss(y_pred, label=labels)#默认reduction='mean' train_cost = cost.numpy()[0] # 反向传播 cost.backward() # 最小化loss，更新参数 optimizer.step() # 清除梯度 optimizer.clear_grad() if epoch_id%5 == 0: #训练轮数为500，每5轮保存一次参数 print("Pass:%d,Cost:%0.5f"%(epoch_id, train_cost)) # save state_dict paddle.save(model.state_dict(),'./checkpoint/epoch{}.pdparams'.format(epoch_id)) paddle.save(optimizer.state_dict(),'./checkpoint/epoch{}.pdopt'.format(epoch_id)) train_num = train_num + BATCH_SIZE train_nums.append(train_num) train_costs.append(train_cost) train(model)登录后复制

绘制模型训练过程图

In [15]

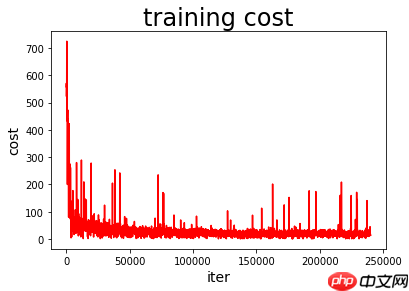
def draw_train_process(iters, train_costs): plt.title("training cost", fontsize=24) plt.xlabel("iter", fontsize=14) plt.ylabel("cost", fontsize=14) plt.plot(iters, train_costs, color='red', label='training cost') plt.show() matplotlib.use('TkAgg') %matplotlib inline draw_train_process(train_nums, train_costs)登录后复制

6.5 模型预测

我们将首先加载存储的参数到模型中，接着使用该模型及其相关参数对测试数据集进行回归效果评估。

评价指标包括预测值和真实值的均方差（mean_loss）和预测值和真实值的相关系数（corr）

通过绘制epoch v.s. loss图以及epoch v.s. corr图，直观查看训练过程中loss和corr的变化

通过寻找最低loss的函数记录最佳的epoch_id，并保存到最佳参数目录

通过寻找最高corr的函数记录最佳的epoch_id，并保存到最佳参数目录 In [16]

#对测试数据集的预测结果进行评价batch=[] loss=[] corr=[]for batch_id in range(0,500,5):#训练轮数为500，每5轮保存一次参数 # 加载模型参数 layer_state_dict = paddle.load('checkpoint/epoch{}.pdparams'.format(batch_id)) opt_state_dict = paddle.load('checkpoint/epoch{}.pdopt'.format(batch_id)) optimizer = paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters()) model.set_state_dict(layer_state_dict) optimizer.set_state_dict(opt_state_dict) # 获取预测数据 INFER_BATCH_SIZE = 100 #len(test_data) infer_features_np = np.array([data[:13] for data in test_data]).astype("float32") infer_labels_np = np.array([data[-1] for data in test_data]).astype("float32") infer_features = paddle.to_tensor(infer_features_np) infer_labels = paddle.to_tensor(infer_labels_np) fetch_list = model(infer_features) sum_cost = 0 for i in range(INFER_BATCH_SIZE): infer_result = fetch_list[i][0] ground_truth = infer_labels[i] #if i % 10 == 0: #print("No.%d: infer result is %.2f,ground truth is %.2f" % (i, infer_result, ground_truth)) cost = paddle.pow(infer_result - ground_truth, 2) sum_cost += cost mean_loss = sum_cost / INFER_BATCH_SIZE #计算均方差 x = pd.Series(np.array(fetch_list.flatten()).tolist()) #利用Series将列表转换成新的、pandas可处理的数据 y = pd.Series(infer_labels_np.tolist()) xycorr = round(x.corr(y), 4) #计算相关系数，round(a, 4)是保留a的前四位小数 print("epoch_id:%d, Mean loss is:%.4f, corr is:%.4f"%(batch_id, mean_loss.numpy(),xycorr)) if mean_loss.numpy()<30 : batch=np.append(batch,batch_id) loss=np.append(loss,mean_loss.numpy()) corr=np.append(corr,xycorr)登录后复制 In [18]

#绘制epoch v.s. loss图def plot_epoch_loss(batch, loss): plt.figure() plt.title("epoch v.s. loss", fontsize=24) plt.xlabel("epoch_id", fontsize=14) plt.ylabel("loss", fontsize=14) plt.ylim(0,30) plt.scatter(batch, loss, alpha=0.5) # scatter:散点图,alpha:"透明度" #plt.plot(ground, ground, c='red') plt.show()登录后复制 In [19]

#绘制epoch v.s. corr图def plot_epoch_corr(batch, corr): plt.figure() plt.title("epoch v.s. corr", fontsize=24) plt.xlabel("epoch_id", fontsize=14) plt.ylabel("corr", fontsize=14) plt.ylim(0,1) plt.scatter(batch, corr, alpha=0.5) # scatter:散点图,alpha:"透明度" #plt.plot(ground, ground, c='red') plt.show()登录后复制 In [20]

plot_epoch_loss(batch, loss) # 记录最佳位置print ('loss最佳epoch位置：', int(batch[loss.tolist.index(min(loss))])) plot_epoch_corr(batch, corr) # 记录最佳位置print ('corr最佳epoch位置：', int(batch[corr.tolist.index(max(corr))])) import os from shutil import copy file_path = 'best model{nowTime}' # 或者可以使用hourTime或dayTime，根据需要选择。isExists = os.path.exists(file_path) if not isExists： os.makedirs(file_path ) copy('checkpoint/epoch{}.pdparams'.format(zuijia), file_path ) copy('checkpoint/epoch{}.pdopt'.format(zuijia), file_path ) copy('checkpoint/epoch{}.pdparams'.format(zuijia, file_path ) copy('checkpoint/epoch{}.pdopt'.format(zuijia, file_path )

7.模型应用

导入需要应用模型进行预测的数据

对导入的数据按第5部分的预处理方法进行预处理

加载模型的最佳参数，对数据进行预测，评估预测结果

把预测值和实际值进行可视化处理

In [21]

# 从文件导入应用数据datafile = './yingyong.data'yingyong_data = np.fromfile(datafile, sep=' ') feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV'] feature_num = len(feature_names)# 将原始数据进行Reshape，变成[N, 14]这样的形状yingyong_data = yingyong_data.reshape([yingyong_data.shape[0] // feature_num, feature_num])#！！归一化程序务必与第5部分所使用的完全一致！！只对属性进行归一化yingyong_features = feature_norm(yingyong_data[:, :13]) # print(feature_trian.shape)yingyong_data = np.c_[yingyong_features, yingyong_data[:, -1]].astype(np.float32)# print(training_data[0])登录后复制 In [22]

# load 最佳的参数batch_id=zuijia #zuijia1 !!!根据显示的epoch位置调整!!!layer_state_dict = paddle.load('best model2021-11-19 12:17:58/epoch270.pdparams')#layer_state_dict = paddle.load('checkpoint/epoch{}.pdparams'.format(batch_id))opt_state_dict = paddle.load('checkpoint/epoch{}.pdopt'.format(batch_id)) model.set_state_dict(layer_state_dict) optimizer.set_state_dict(opt_state_dict) # 获取预测数据INFER_BATCH_SIZE = len(yingyong_data) infer_features_np = np.array([data[:13] for data in yingyong_data]).astype("float32") infer_labels_np = np.array([data[-1] for data in yingyong_data]).astype("float32") infer_features = paddle.to_tensor(infer_features_np) infer_labels = paddle.to_tensor(infer_labels_np) fetch_list = model(infer_features) sum_cost = 0for i in range(INFER_BATCH_SIZE): infer_result = fetch_list[i][0] ground_truth = infer_labels[i] if i % 1 == 0: print("No.%d: infer result is %.2f,ground truth is %.2f" % (i, infer_result, ground_truth)) cost = paddle.pow(infer_result - ground_truth, 2) sum_cost += cost mean_loss = sum_cost / INFER_BATCH_SIZEprint("Mean loss is:", mean_loss.numpy())登录后复制 In [23]

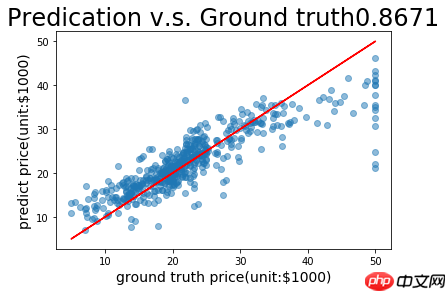
x = pd.Series(flatten(fetch_list).tolist) y = pd.Series(infer_labels_np.tolist)计算相关系数：x与y间的相关系数为xxcorr，保留四位小数。

def plot_pred_ground(pred, ground): plt.figure() plt.title("Predication v.s. Ground truth"+ str(xycorr), fontsize=24) plt.xlabel("ground truth price(unit:$1000)", fontsize=14) plt.ylabel("predict price(unit:$1000)", fontsize=14) plt.scatter(ground, pred, alpha=0.5) # scatter:散点图,alpha:"透明度" plt.plot(ground, ground, c='red') plt.show() plot_pred_ground(fetch_list, infer_labels_np)登录后复制

8. 心得体会

利用这款研究工具，我对比了每次迭代前，先对训练数据进行随机打乱np.random.shuffle(train_data)与不进行该操作两种方法的效果，并深入理解了机器学习与传统模型之间的差异。

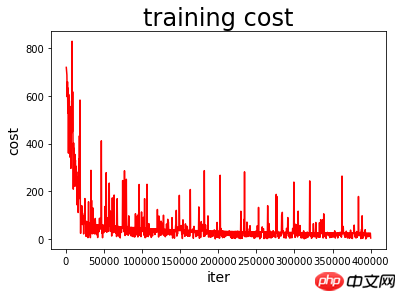
若不随机打乱训练数据顺序，传统的拟合过程表现为均方差loss持续下降，显示拟合效果不断优化。然而，将模型应用于测试集后却出现显著的loss变化，表明模型泛化能力不足，导致预测结果偏差大。

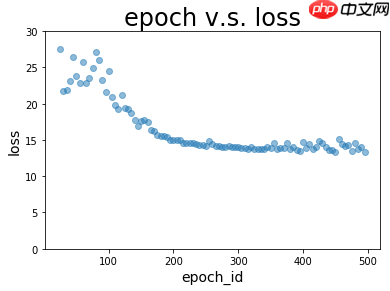
若对训练数据的顺序进行随机的打乱，程序执行的是机器学习过程，在此过程中均方差（MSE）损失值呈现波动下降趋势。每次打乱顺序后，loss都会出现短暂的脉冲变化，但经过模型优化处理，这些波动会逐渐平息并最终导致loss持续下降。当加载训练好的模型及参数对测试集进行预测时，观察到loss值非常低，并且在变化不大的区间内，这表明模型对新数据的泛化能力得到了显著提升，从而验证了优化后的模型性能的有效性。

以上就是基于PaddlePaddle2.2的数据建模研究助手的详细内容，更多请关注其它相关文章！